Rasterización - Color Shading #

1. Introducción #

En este parte del taller se busca aplicar las coordenadas baricéntricas para la rasterización de una primitiva, como lo es un triángulo, además este sistema de coordenadas se usa para determinar el color en un punto dentro del tríangulo permitiendo crear un degrado entre los distintos colores que tiene cada uno de los vértices.

2. Revisión bibliográfica #

Rasterización #

La rasterización es el proceso por el cual una primitiva o un gráfico vectorial se transforma en una imagen bidimensional o en un conjunto de píxeles, que luego serán mostrados en pantalla. Dicho proceso consta de dos partes:

La primera, determina que cuadrados de una cuadricula están siendo ocupados por la primitiva
Asignar el color y profundidad a cada cuadrado.

Coordenadas baricéntricas #

Es un sistema de coordenadas en el cual un punto dentro de un triángulo se puede representar mediante pesos, de modo que e punto se puede interpretar como un centro de masa.

Considere un triángulo cuyos vertices son \(A=(x_0, y_0), B=(x_1, y_1), C=(x_2, y_2)\) y un punto \(p\) . Entonces, el punto \(p\) se puede representar como:

\[p = \alpha A + \beta B + \gamma C\]

Se tiene que un punto está dentro del triángulo si y solo si: \[0 < \alpha < 1\] \[0 < \beta < 1\] \[0 < \gamma < 1\]

Los pesos que antes se mencionaron se pueden calcular de la siguiente manera:

\[P_x = W_{v0}X_{v0} + W_{v2}X_{v2} + W_{v2}X_{v2}\]

\[P_y = W_{v0}Y_{v0} + W_{v2}Y_{v2} + W_{v2}Y_{v2}\] \[W_{v0} + W_{v0} + W_{v2} = 1\]

Una aplicación de las coordenadas baricéntricas es la interpolación de colores, es decir, determinar el color de un punto dentro de un triángulo, para esto se cualcular de la siguiente manera:

\[C = \alpha C_A + \beta C_B + \gamma C_C\]

Cabe mencionar que cada uno de los colores \(C_A, C_B, C_C\) es un vector de 3 componentes, \((R, G, B)\) .

La interpolación de colores se puede realizar también de la siguiente manera mediante los pesos mencionados anteriormente:

\[Color_p = \frac{W_{v0}Color_{v0} + W_{v1}Color_{v1} + W_{v2}Color_{v2}}{W_{v0} + W_{v1} + W_{v2}}\]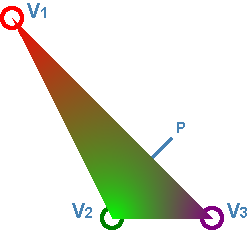 Color interpolation

3. Métodos #

Para la realización de este tema hicimos uso de los conceptos anteriormente expuestos junto con la libreria de p5.quadrille.js, de tal forma que se presenta una implementación de la rasterización de un triángulo con color shading por medio de las coordenadas baricéntricas.

4. Resultados #

Instrucciones

Al presionar cualquier tecla, se mostrará un nuevo triángulo aleatorio.
Al pasar por encima de una celda, se mostará el color de dicha celda.

Código


let quadrille;
let ROWS, COLS, LENGTH;
let x0, y0, x1, y1, x2, y2;
let v0Color, v1Color, v2Color;
let slider, colorPick = [6, 6, 23];

function setup(){
    createCanvas(500, 500);
    frameRate(10);
    slider = createSlider(5, 100, 25, 5);
    slider.position(25, 25);

    quadrille = createQuadrille(ROWS, COLS);

    v0Color = createColorPicker(color('#f6d265'));
    v1Color = createColorPicker(color('#2a65b4'));
    v2Color = createColorPicker(color('#cc0a30'));

    v0Color.position(180, 20);
    v1Color.position(240, 20);
    v2Color.position(300, 20);

    v0Color.input(() => { quadrille.colorizeTriangle(x0, y0, x1, y1, x2, y2, v0Color.color(), v1Color.color(), v2Color.color()) });
    v1Color.input(() => { quadrille.colorizeTriangle(x0, y0, x1, y1, x2, y2, v0Color.color(), v1Color.color(), v2Color.color()) });
    v2Color.input(() => { quadrille.colorizeTriangle(x0, y0, x1, y1, x2, y2, v0Color.color(), v1Color.color(), v2Color.color()) });

    quadrilleZoom();
    slider.changed(quadrilleZoom);

    randomTriangle();
}

function draw(){
    background('#060621');
    drawQuadrille(quadrille, { cellLength: LENGTH, outlineWeight: 0.5, outlineColor: color('green'), board: false });
    tri();
    setText();
    pickColor();
}

function randomTriangle(){

    x0 = int(random(0, ROWS));
    y0 = int(random(0, COLS));
    x1 = int(random(0, ROWS));
    y1 = int(random(0, COLS));
    x2 = int(random(0, ROWS));
    y2 = int(random(0, COLS));

    quadrille.clear();
    quadrille.colorizeTriangle(x0, y0, x1, y1, x2, y2, v0Color.color(), v1Color.color(), v2Color.color());
}

function keyPressed(){
    randomTriangle();
}

function tri() {
    push();
    stroke('cyan');
    strokeWeight(2);
    noFill();
    triangle(y0 * LENGTH + LENGTH / 2, 
             x0 * LENGTH + LENGTH / 2, 
             y1 * LENGTH + LENGTH / 2, 
             x1 * LENGTH + LENGTH / 2, 
             y2 * LENGTH + LENGTH / 2, 
             x2 * LENGTH + LENGTH / 2
    );
    pop();
}

function quadrilleZoom(){
    aux1 = ROWS;
    aux2 = COLS;

    COLS = slider.value();
    LENGTH = int(width / COLS);
    ROWS = int(height / LENGTH);

    quadrille = createQuadrille(COLS, ROWS);

    x0 = round(map(x0, 0, aux1, 0, ROWS));
    y0 = round(map(y0, 0, aux2, 0, COLS));
    x1 = round(map(x1, 0, aux1, 0, ROWS));
    y1 = round(map(y1, 0, aux2, 0, COLS));
    x2 = round(map(x2, 0, aux1, 0, ROWS));
    y2 = round(map(y2, 0, aux2, 0, COLS));

    quadrille.colorizeTriangle(x0, y0, x1, y1, x2, y2, v0Color.color(), v1Color.color(), v2Color.color());
}

function setText(){

    fill(colorPick);
    rect(370, 12, 110, 25, 2)
    noStroke();

    fill(255);
    text(colorPick.toString(), width - 75, 30)
    textSize(16);
    textAlign(CENTER);
}

function pickColor(){
    let x = mouseX;
    let y = mouseY;

    let colCell = floor(x / LENGTH);
    let rowCell = floor(y / LENGTH);


    let cellInfo = quadrille.read(rowCell, colCell)

    cellInfo
    ? colorPick = ([cellInfo.levels[0], cellInfo.levels[1], cellInfo.levels[2]])
    : colorPick = [6, 6, 23];
    
}

Conclusiones #

Como trabajo futuro se puede implementar el anti-aliasing para mejorar la calidad de la imagen y así evitar el efecto de escalonamiento.