Aplicación de las rotaciones y traslaciones de objetos 3D #

1. Introducción #

En este punto del taller se busca hacer uso de las transformaciones (rotaciones y traslaciones) de objetos 3D, por medio de la construccion de una ilusion optica llamada la ventana de Amés.

2. Revisión bibliográfica #

Traslación #

La translación de un objeto consiste en moverlo cierta distancia, en una dirección determinada. En 3D, el sistema de referencia homogéneo tendrá 4 dimensiones, por lo que la traslación del punto \( V = (x,y,z,1) \) quedará indicada como :

\( V' = (x',y',z',1) = (x,y,z,1) \; \cdot \; \bold{T} \)

Donde \( \bold{T} \) sera la matrix de traslación en 3D y \( (T_x, T_y , T_z) \) correspondera al vector de traslación:

\( T = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ T_x & T_y & T_z & 1 \end{bmatrix} \)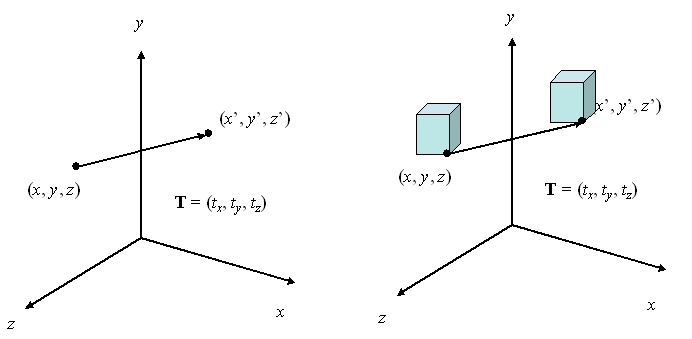

Rotación #

La rotación en tres dimensiones puede definirse alrededor de cualquier recta en el espacio. Existen tres rotaciones elementales que se definen alrededor de los ejes coordenados. Las matrices de rotacion correspondientes a estos son las siguientes.

\( R_x = \begin{bmatrix} \cos \theta & \sin \theta & 0 & 0 \\ -\sin \theta & \cos \theta & 0 & 0\\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \) \(R_y = \begin{bmatrix} \cos \theta & 0 & -\sin \theta & 0 \\ 0 & 1 & 0 & 0 \\ \sin \theta & 0 & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \\ \\\) \(R_z = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \theta & \sin \theta & 0 \\ 0 & -\sin \theta & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \)

Ventana de Ames #

Inventada por el oftalmólogo estadounidense Adelbert Ames, Jr en 1951 y consiste en una ventana que está hecha de forma que, cuando se observa frontalmente, parece una ventana rectangular, pero en realidad es un trapecio. La ilusión consiste en un efecto visual de una ventana que parece se estuviera balanceando de un lado hacia el otro cuando, en realidad, gira provocando un cambio en la percepción de su tamaño.

Sin embargo, a pesar de saber que la ventana está girando y no realizando un balanceo y, además conocer qué es un trapecio y no un rectángulo, a nuestro cerebro le es imposible romper la ilusión óptica y continuamos observando un balanceo de tan solo 180 grados.

3. Métodos #

Con el fin de usar los conceptos anteriormente expuestos, se construye una escena usando la libreria ThreeJs, en la cual crearemos la ventana de Ames en base a boxGeometry y se le aplicaran las transformaciones necesarias para que se vea lo mas parecida posible a la ventana de Ames. Debido a la naturaleza de la ilusión, se debe de usar una camara ortografica para que no se distorsione la imagen.

4. Resultados #

Código


var boxArray = [];
var group;
var camera, scene, renderer, webGlCanvas;
var ball, ruler, light, rotationFlag;
const thickness = 0.1;

function initialize() {
    rotationFlag = true;
	scene = new THREE.Scene();

	camera = new THREE.OrthographicCamera(
		10 / -2,
		10 / 2,
		10 / 2,
		10 / -2,
		1,
		150
	);
	camera.position.z = 10;

	webGlCanvas = document.getElementById("webGlDiv");
	renderer = new THREE.WebGLRenderer();
	renderer.setSize(700, 700);
	webGlCanvas.appendChild(renderer.domElement);

	initBoxes();

	group = new THREE.Group();

	for (var i = 0; i < boxArray.length; i++) {
		group.add(boxArray[i]);
	}

	scene.add(group);
    
	createBall();
	createRuler();
	initButtons();
	animate();
}

function initBoxes() {
	const thickness = 0.1;
	const texture = new THREE.MeshBasicMaterial({ color: 0x00ff00 });

	const box1 = new THREE.BoxGeometry(6, thickness * 2, thickness * 5);
	const box2 = new THREE.BoxGeometry(6, thickness * 2, thickness * 5);
	const box3 = new THREE.BoxGeometry(thickness * 2, 1.7, thickness * 5);
	const box4 = new THREE.BoxGeometry(thickness * 2, 3.79, thickness * 5);
	const box5 = new THREE.BoxGeometry(5.8, thickness * 2, thickness * 5);
	const box6 = new THREE.BoxGeometry(2.2, thickness * 2, thickness * 5);
	const box7 = new THREE.BoxGeometry(2.9, thickness * 2, thickness * 5);

	const cube = new THREE.Mesh(box1, texture);
	const cube2 = new THREE.Mesh(box2, texture);
	const cube3 = new THREE.Mesh(box3, texture);
	const cube4 = new THREE.Mesh(box4, texture);
	const cube5 = new THREE.Mesh(box5, texture);
	const cube6 = new THREE.Mesh(box6, texture);
	const cube7 = new THREE.Mesh(box7, texture);

	cube.position.set(0, 1.3, 0);
	cube2.position.set(0, -1.3, 0);
	cube3.position.set(-2.88, 0, 0);
	cube4.position.set(2.87, 0, 0);
	cube5.position.set(0, 0, 0);
	cube6.position.set(-1.3, 0, 0);
	cube7.position.set(0.7, 0, 0);

	cube6.rotation.z = (Math.PI * 1) / 2;
	cube7.rotation.z = (Math.PI * 1) / 2;
	cube.rotation.z = 0.175;
	cube2.rotation.z = -0.175;

	boxArray.push(cube);
	boxArray.push(cube2);
	boxArray.push(cube3);
	boxArray.push(cube4);
	boxArray.push(cube5);
	boxArray.push(cube6);
	boxArray.push(cube7);
}

function animate() {
	requestAnimationFrame(animate);
	rotateObjects();
	renderer.render(scene, camera);
}

function createBall() {
	ball = new THREE.SphereGeometry(thickness * 4, 32, 32);
	const ballMaterial = new THREE.MeshBasicMaterial({ color: 0x0000ff });

	ball = new THREE.Mesh(ball, ballMaterial);
	ball.position.set(-3.2, 1, 0);
    ball.visible = false;
	group.add(ball);
}

function createRuler() {
	box = new THREE.BoxGeometry(5, thickness, thickness * 3);
	const rulerMaterial = new THREE.MeshBasicMaterial({ color: 0xff0000 });

	ruler = new THREE.Mesh(box, rulerMaterial);

	ruler.position.set(0, 0.3, 0);
	ruler.rotation.y = Math.PI / 2;
	ruler.rotation.z = Math.PI / 9;
    ruler.visible = false;
	scene.add(ruler);
}

function rotateObjects(){
    if(rotationFlag){
        group.rotation.y += 0.02;
	    ruler.rotation.y += 0.02;
    }
}

function initButtons() {
	document.getElementById("ball").addEventListener("click", function () {
		ball.visible = !ball.visible;
	});
	document.getElementById("ruler").addEventListener("click", function () {
		ruler.visible = !ruler.visible;
	});
    document.getElementById("rotation").addEventListener("click", function () {
        rotationFlag = !rotationFlag;
    });
}

initialize();